통계의 꽃이라고도 불리는 중심극한정리,
정신없이 공부를 해가다보면 이전에 배웠던 내용들을 계속 까먹게되고, 결국 누군가 '중심극한정리가 뭐야?', '신뢰구간이 뭐야?'라고 내게 물을 때 자신있게 대답할 수가 없게 된다. 그래서 잊지 않으려고 나만의 언어로 중심극한정리와 신뢰구간을 정리해보았다.
중심극한정리
"표본(샘플) 크기가 충분히 크다면(일반적으로 n >= 30) 표본평균은 모평균을 평균으로 하고, 모분산/n을 분산으로 하는 정규분포에 근사한다. "
1000번 가량 표본을 추출하는 상황을 가정해보자. 이 때 한 번 추출하는 표본의 수가 n=3, n=50, n=100 이런 식으로 커지면 커질수록 정규분포에 더 가깝게 수렴하게 된다. (한 번 추출하는 표본 수가 작더라도 표본을 추출하는 횟수가 커지면 커질수록 정규분포에 근사한다.)
중요한 점은 모집단의 분포가 정규분포를 따르지 않더라도 표본크기가 충분히 크다면 표본평균은 정규분포를 따르게 된다는 점이다. (모집단이 정규분포를 따른다면 표본평균은 정규분포를 따르는 X들의 선형결합이므로 당연히 정규분포를 따른다) 아래 그림 중 첫번째 Bin(10, 0.9) 분포를 보면 n=30, n=100인 경우 평균이 9.0 (이항분포에서 모평균은 n * p)인 정규분포에 근사하고 있음을 알 수 있다.
참고로 큰 수의 법칙(Law of Large Number, LLN)과 중심극한정리를 혼동하는 경우가 많은데, 이 부분을 짚고 넘어가자. 큰 수의 법칙은 "표본의 크기가 커지면 표본평균이 모평균에 가까워짐을 의미한다." 즉, 표본의 수를 0 -> 무한대 이런 식으로 계속해서 쌓아가며 늘리면 결국 그 표본의 평균은 모평균에 가까워진다는 뜻이다. 큰 수의 법칙은 정규분포에 관한 내용은 전혀 이야기하고 있지 않다.

신뢰구간
신뢰구간과 중심극한정리를 같은 포스팅에 넣은 것은 선자의 바탕이 후자가 되기 때문이다.
현재 재학 중인 고려대 경영대 학생들의 평균 학점을 알고 싶다고 하자. 여기서 모집단은 현재 재학 중인 경영대생 전체이다. 이 중 100명을 뽑아 평균을 내었는데 약 3.5가 나왔다. 이 때 이 표본평균은 점 추정치(Point Estimator)이다. (딱, 한 숫자로 추정한다) 점 추정 방식은 간단하지만 추정의 정확도에 관한 정보는 전혀 주지 못한다는 점에서 단점이 존재한다. 결국 우리가 샘플로 알고 싶은 건 모집단의 특성인데, 샘플이 달라짐에 따라 표본평균이 달라지게 될 것이니 딱 한 포인트로 평균을 이야기하는 것보다는 어떤 바운더리 안에 모평균이 포함될 확률이 95%다라는 식으로 이야기해주는 게 더 정확한 정보를 제공하는 것이라 할 수 있겠다. 이런 방식을 구간 추정(Interval Estimation)이라고 한다.
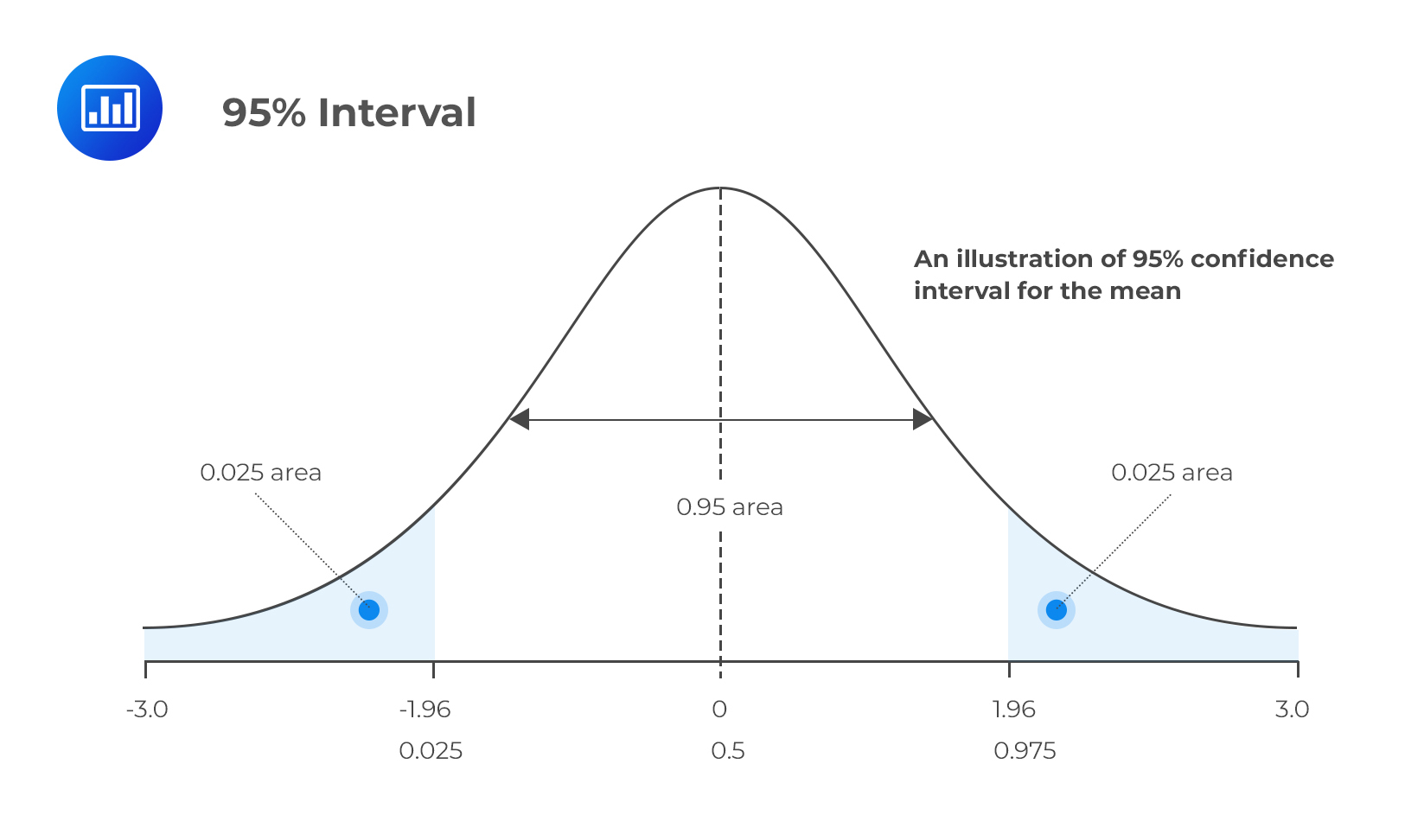
출처 : analystprep.com
위 그림 익숙하시죠? 네, 맞습니다. 표준정규분포입니다. 평균이 0이고, 분산이 1인 정규분포입니다. 앞선 중심극한정리에 따르면 표본크기가 충분히 크다면 (보통 n이 30 이상) 표본평균은 평균이 mu(모평균)이고, 분산이 sigma^2/n 인 정규분포를 따르게 됩니다. 이걸 표준화해준다면 위와 같은 분포가 나오겠지요. 저 그림 속 0은 표본평균과 모평균 mu가 같아지는 지점을 의미합니다. n이 커지면 커질수록 표본평균의 분산이 0에 가까워질테니 표본평균-모평균도 0에 가까워지게 됩니다.
신뢰구간은 현재 나의 표본평균을 가지고 산정한 모평균이 포함된 바운더리입니다. 아래 식을 보시죠.
표본평균 - z* sigma/n^1/2 는 모평균의 lower bound를, 표본평균 + sigma/n^1/2 는 모평균의 upper bound를 의미합니다. 이 구간을 우리는 신뢰구간이라고 부릅니다. 여기서 z는 신뢰구간의 범위를 결정하는 계수, 즉 confidence coeffient이며, 몇 %의 확률로 해당 구간에 모평균이 포함되어있는지를 결정합니다. 위 그림에서 평균 0으로부터 95% 신뢰구간을 찾는 경우 z는 1.96이 됩니다.
예를 들어 설명해보겠습니다. 고려대 졸업생의 평균 나이를 측정하고자 30명의 임의표본을 추출했습니다. 그 결과 평균나이는 31.8세, 표준편차는 4.3세였습니다. 이를 바탕으로 신뢰구간을 산출한 결과 평균에 대한 95% 신뢰구간은 [30.2, 33.4]였습니다. 즉, 샘플을 100번 뽑는다면 그 중 95번은 모평균이 30.2세와 33.4세 사이에 있습니다.
출처: 나부랭이의 수학블로그
주의해야할 점은 표본의 크기가 작은 경우에는 z 값을 사용할 수 없다는 것입니다. n이 충분히 크지 않아 표본평균이 정규분포를 따르지 않기 때문이죠. 하지만 괜찮습니다. 이 때는 (표본평균 - 모평균) / (표준오차) 가 스튜던트 t 분포를 따르게 되기 때문에 t-분포를 이용해 z값이 아닌 t값으로 신뢰구간의 계수를 사용하면 됩니다.
(t-분포도 결국 표본 수가 커질수록 정규분포에 수렴하게 됩니다)

'🥐데이터분석' 카테고리의 다른 글
| 다중회귀분석 R-squared 가 낮아도(0.2, 0.3) 괜찮을까? (0) | 2021.09.14 |
|---|---|
| 분류모델 성능평가 지표 : Confusion Matrix (0) | 2021.09.11 |
| Bias-Variance Trade off(편향-분산 트레이드오프/ 딜레마)란? (0) | 2021.09.09 |
| Hierarchical Bayesian model (베이지안 계층모형) (0) | 2021.08.19 |
| MCMC를 이용한 베이지언 추정(Bayesian Estimation) (0) | 2021.08.19 |
