현재 두 가지 분석프로젝트를 진행하고 있는데, 그 중 한 프로젝트 미팅을 진행하던 중 아래와 같은 질문들을 받게 되었다.
해당 프로젝트의 초반 단계에 관해 간략히 설명하자면 다중회귀분석 및 기타 변수 선택 방법들을 이용하여 택배 중고거래와 유의미한 관계가 있는 변수를 선택한 후, 선택된 변수들을 이용하여 클러스터링을 진행하여 최적 입지 선정을 위한 1차 입지(자치구)를 선정한다.
서울 자치구 25개로 다중회귀분석을 진행하였는데, 샘플사이즈가 작은 것 같다, 그래도 괜찮은가?
보통 독립변수 1개 당 표본 5-10개 정도가 경험적으로(Rules of Thumb) 괜찮은 정도로 이야기되지만 학자들마다 의견이 분분하다. 실제 연구를 진행할 때는 연구자가 효과크기(effect size) 및 유의수준을 고려한 통계적 검정력을 기준으로 적합한 최소 표본크기를 정한다고 한다. 다중회귀분석의 경우 통계적 검정력을 0.8 이상으로 유지하기 위해서는 표본크기가 최소 50이상이 되어야 한다고 주장하는 견해도 있고, 앞서 말했듯 독립변수와 표본크기의 비율로서 접근하여 1:5~20 정도로 이야기하는 경우도 많다.
찾아보니 Green(1991)의 연구결과가 많이 사용되는 듯하다. Green은 모델의 전반적인 핏을 테스트할 지(R-squared)와 각 변수의 회귀계수를 테스트 할 지에 따라 최소 표본크기를 다르게 제안하고 있다. 전자의 경우 최소 50 + 8k개(k는 독립변수 수), 후자의 경우 최소 104 + k개가 필요하다고 말한다.
결론 : 기존에 했던대로 424개 행정동 단위로 진행하는 것이 나을 듯하다.
cf) 왜 표본이 작으면 회귀계수가 유의하지 않게 되는걸까?
회귀계수 Beta^의 분산을 살펴보면 분자에 오차의 분산이 있는 것을 알 수 있다. 즉, 오차의 분산이 작아지면 작아질수록 회귀계수의 분산 역시 작아지게 된다. 그럼 오차의 분산은 어떻게 이루어져 있는가? 오차의 분산이 실현된 것이 결국 잔차의 분산인데 이는 잔차의 제곱합(SSE)을 n-2로 나누어준 값이 바로 잔차의 분산이 된다. (잔차의 평균은 0이므로 잔차제곱합은 결국 편차(각 잔차에서 0을 뺌)제곱의 합과 같다) 이 잔차의 분산은 n이 커지면 커질수록 작아지니, 결론적으로 회귀계수의 분산도 n이 커질수록 작아지게 되고, 이로 인해 회귀계수의 p-value가 작아지게 되면서 귀무가설(beta = 0)을 기각하게 될 가능성이 높아진다.

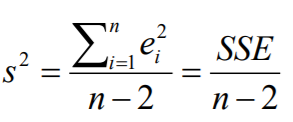
424개 행정동으로 다중회귀분석을 진행했을 때는 Adj.R-Squared 가 0.23 정도로 매우 낮다, 그러나 몇몇 유의한 변수들이 보인다, 0.23 정도의 r-squared로 이 변수들을 선택해도 괜찮은가?
다중회귀분석의 두 가지 key elements가 있는데, R-squared와 Coefficients(회귀계수)이다. 일반적으로 R-squared 보다는 특정 독립변수가 종속변수의 변동을 유의미하게(statistically significant) 설명하는지의 여부가 더 중요하다고 판단된다. 일반적으로 인문사회과학쪽에서는 R-squared가 0.2,0.3 정도도 괜찮은 값이라고 생각한다고 한다. 물론 예측을 목적으로 사용하는 것이 아닌 가설을 검증하는 차원에서 말이다. 만약 독립변수와 종속변수의 관계를 설명하는 것이 주 목적이라면 R-squared 가 낮은 것보다도 회귀계수가 유의한지가 더 중요할 수 있다. 반면, 예측이 목적이라면 R-squared는 중요한 지표가 된다. R-squared는 내가 가진 독립변수들로 종속변수의 변동을 얼마나 설명할 수 있느냐를 뜻하기 때문에, 결국 R-squared가 높으면 높을수록 내가 만든 모델로 종속변수를 더 정확하게 예측할 수 있게 된다.
결론 : 행정동 단위로 진행 시 비록 R-squared가 0.2 정도였지만, 유의한 변수들이 나왔으니 이 방식대로 디벨롭해보겠다.
클러스터링에 사용되는 세 변수 중 두 개가 연령대인데, 그럼 결국 인구가 많은 곳이 선택되는 것이 아닌가?
자치구 단위로 후진소거법(Backward Elimination)을 진행하였을 때 유의하게 나온 변수는 30대와 10대 였다. (클러스터링 시 다른 변수도 추가했다) 두 변수의 상관관계는 0.76으로 매우 강했는데, 회귀분석을 진행하기 전 Box-Cox 변환 후 표준화를 하여 결론적으로 두 변수간의 다중공선성 문제는 존재하지 않게 되었다. 결론적으로 강남구, 송파구, 강서구가 선택이 되었는데 다른 연령대로 바꾸어해봐도 결과가 같았으며, 그 이유는 결국 이 세 구의 인구수가 기본적으로 가장 많기 때문이다. (주민등록기준 송파구 67만명 > 강서구 61만명 > 강남구 56만명으로 서울 자치구 인구수 TOP3)
결론 : 분석결과가 이렇게 나온 것이기는 하지만 실질적으로 큰 인사이트가 없다고 느껴질 수 있기 때문에 다시 한 번 분석을 수정해보려고 한다.
'🥐데이터분석' 카테고리의 다른 글
| [토픽 모델링] LDA(Latent Dirichlet Allocation) 개념 설명👀 (0) | 2022.06.07 |
|---|---|
| [토픽 모델링] 기본 개념 이해하기 😎 (0) | 2022.06.06 |
| 분류모델 성능평가 지표 : Confusion Matrix (0) | 2021.09.11 |
| 중심극한정리(Central Limit Theorem), 신뢰구간(Confidence Interval) (0) | 2021.09.10 |
| Bias-Variance Trade off(편향-분산 트레이드오프/ 딜레마)란? (0) | 2021.09.09 |